Basic Mathematics
Number System LCM & HCF Percentage Ratio & Proportion Average Simple InterestBusiness Mathematics
Profit & Loss Compound Interest Partnership Discount Stocks & Shares BankingTime, Work & Motion
Time & Work Pipes & Cisterns Time, Speed & Distance Trains Boats & Streams RacesAdvanced Mathematics
Algebra Geometry Mensuration Trigonometry Logarithms & Indices Coordinate GeometryStatistics & Probability
Statistics Probability Permutation Combination Set Theory Data InterpretationSet Theory Aptitude Questions & Formulas with answer
Ques 1 GATE 2024 SET-2
In an engineering college of 10,000 students, 1,500 like neither their core branches nor other branches. The number of students who like their core branches is 1/4th of the number of students who like other branches. The number of students who like both their core and other branches is 500. The number of students who like their core branches is
(d) is the correct answer.
Ques 2 GATE 2019
In a college, there are three student clubs. Sixty students are only in the Drama club, 80 students are only in the Dance club, 30 students are only in the Maths club, 40 students are in both Drama and Dance clubs, 12 students are in both Dance and Maths clubs, 7 students are in both Drama and Maths clubs, and 2 students are in all the clubs. If 75% of the students in the college are not in any of these clubs, then the total number of students in the college is
(c) is the correct answer.
Ques 3 GATE 2018
To pass a test, a candidate needs to answer at least 2 out of 3 questions correctly. A total of 6,30,000 candidates appeared for the test. Question A was correctly answered by 3,30,000 candidates. Question B was answered correctly by 2,50,000 candidates. Question C was answered correctly by 2,60,000 candidates. Both questions A and B were answered correctly by 1,00,000 candidates. Both questions B and C were answered correctly by 90,000 candidates. Both questions A and C were answered correctly by 80,000 candidates. If the number of students answering all questions correctly is the same as the number answering none, how many candidates failed to clear the test?
(d) is the correct answer.
Ques 4 GATE 2018
To pass a test, a candidate needs to answer at least 2 out of 3 questions correctly. A total of 6,30,000 candidates appeared for the test. Question A was correctly answered by 3,30,000 candidates. Question B was answered correctly by 2,50,000 candidates. Question C was answered correctly by 2,60,000 candidates. Both questions A and B were answered correctly by 1,00,000 candidates. Both questions B and C were answered correctly by 90,000 candidates. Both questions A and C were answered correctly by 80,000 candidates. If the number of students answering all questions correctly is the same as the number answering none, how many candidates failed to clear the test?
(d) is the correct answer.
Ques 5 GATE 2017 SET-2
500 students are taking one or more courses out of Chemistry. Physics, and Mathematics. Registration records indicate course enrolment as follows: Chemistry (329). Physics (186). Mathematics (295). Chemistry and Physics (83), Chemistry and Mathematics (217), and Physics and Mathematics (63). How many students are taking all 3 subjects?
(d) is the correct answer.
Ques 6 GATE 2016 SET-2
The Venn diagram shows the preference of the student population for leisure activities.
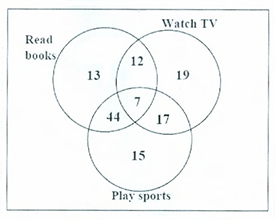
(d) is the correct answer.
Ques 7 GATE 2011
In a class of 300 students in an M.Tech programme, each student is required to take at least one subject from the following three:
M600: Advanced Engineering Mathematics
C600: Computational Methods for Engineers
E600: Experimental Techniques for Engineers
The registration data for the M.Tech class shows that 100 students have taken M600, 200 students have taken C600, and 60 students have taken E600. What is the maximum possible number of students in the class who have taken all the above three subjects?
(d) is the correct answer.
Ques 8 GATE 2010
25 persons are in a room. 15 of them play hockey. 17 of them play football and 10 of them play
both hockey and football. Then the number of persons playing neither hockey nor football is:
(d) is the correct answer.
Ques 9 GATE 2010
25 persons are in a room. 15 of them play hockey, 17 of them play football and 10 of them play both hockey and football. Then the number of persons playing neither hockey nor football is:
(d) is the correct answer.
Ques 10 GATE 2010
A gathering of 50 linguists discovered that 4 knew Kannada, Telugu and Tamil, 7 knew only Telugu and Tamil, 5 knew only Kannada and Tamil, 6 knew only Telugu and Kannada. If the number of linguists who knew Tamil is 24 and those who knew Kannada is also 24, how many linguists knew only Telugu?
(a) is the correct answer.